Reversing a Queue

There was a question in the discussion as to how to reverse a queue without a stack.

Reversing a queue using a stack is quite easy.

 private static void reverseWithStack(Queue<Integer> queue) {
    Stack<Integer> stack = new Stack<Integer>();

    while(queue.isEmpty() == false) {
      stack.push(queue.remove());
    }

    while(stack.isEmpty() == false) {
      queue.add(stack.pop());
    }
  }

How to do it without a stack. I think, there may be convoluted ways. But here's a simple way using recursion:

  private static void reverseWithoutStack(Queue<Integer> queue) {
    if(queue.isEmpty()) {
      return;
    }
    int n = queue.remove();
    reverseWithoutStack(queue);
    queue.add(n);
  }

Well, there's no magic happening here. Actually, we are cheating a bit here. How? We have simulated the behaviour of a stack through recursion. In fact, there's still a stack -- an actual stack -- in action which enables us to solve this problem. It's the program stack! Just that it's hidden.

Many algorithms which could be implemented using a loop and a stack could be rephrased into a simpler one with recursion, simply because recursion hides the stack within itself and allows us to reap its benefits all the same! A classical example is depth first search of trees, which can be implemented using a stack, but a simpler and elegant implementation can be created using recursion.

Here's the complete code:

import java.util.Stack;
import java.util.Queue;
import java.util.LinkedList;

public class Reverse {

  public static void main(String[] args) {

    Queue<Integer> queue = new LinkedList<Integer>();
    queue.add(1);
    queue.add(2);
    queue.add(3);

    System.out.println("Before reversing ...");
    printQueue(queue);
    // reverseWithoutStack(queue);
    reverseWithoutStack(queue);
    System.out.println("After reversing ...");
    printQueue(queue);
  }

  private static void reverseWithStack(Queue<Integer> queue) {
    Stack<Integer> stack = new Stack<Integer>();

    while(queue.isEmpty() == false) {
      stack.push(queue.remove());
    }

    while(stack.isEmpty() == false) {
      queue.add(stack.pop());
    }
  }

  private static void reverseWithoutStack(Queue<Integer> queue) {
    if(queue.isEmpty()) {
      return;
    }
    int n = queue.remove();
    reverseWithoutStack(queue);
    queue.add(n);
  }

  private static void printQueue(Queue<Integer> queue) {
    String s = "[ ";
    for(int i = 0; i < queue.size(); i++) {
      int n = queue.remove();
      if(i <= queue.size() - 1) {
        s += n + ", ";
      }
      else {
        s += n + " ";
      }
      queue.add(n);
    }
    s += "]";
    System.out.println(s);
  }
}

Implementation of Lexical Analyser

Compiler texts usually provide a detailed treatment to the theoretical aspects of the design of a lexical analyser. In most cases, the issues of putting together all these concepts in a real working lexical analyser are typically never discussed. Probably, there’s good reason for this too, as very good tools exist that automatically generate lexical analysers from lexical specifications provided as regular expression patterns.
 

Yet, manually implementing a lexical anlyser that embodies all the concepts taught in a compilers text or course is an interesting engineering exercise. Doing this seems to provide some nuanced insights about how such a system can be designed. Experience thus earned is likely to be useful in solving other software design problems sharing technical properties with the lexical analyser. In this article, we show how a lexical analyser can be implemented using C++. We do so using an example discussed in the following section.

Example

Here, we design a lexical analyser that recognises the follow token classes:

Assignment. (ASSIGN) Represented by the single character ‘=’.
Regular expression: =
Automaton:

Equals. (EQ) Represented by the string ‘==’.
Regular expression: ==
Automaton:

Identifiers. (ID) Represented by any string that starts with an alphabetic character and is followed by zero or more alphanumeric characters.
Regular expression: α[α|N ]?
Automaton:

Whitespace. (WS) Represented by a non-empty string of spaces or tabs.
Regular expression: [SP ACE|T AB]+
Automaton:

A practical recogniser would try to consume as much of the input string as possible returning a token. For instance, if the input in "ab", and the input pointer has just consume ’a’, it has a choice of returning the ID token with lexeme "a". However, the lexer must hang on before hurrying to do that. It must look ahead of where it currently is and decide on its next move based on what it sees. Here, for example, it would see that the next character to be consumed is ’b’. This, if eaten, would help construct a longer lexeme, and result in further progress of the lexical analysis process before a token is returned. Hence, the lexical analyser, instead of returning rightaway will go ahead and consume ’b’. Thereafter, it will find that either the input string is over, or the next unconsumed chanracter is a non-alphanumeric one. Thus, the
lexical analyser will return ID token class "ab" being the lexeme.

Combining the Automata

There are multiple approaches possible in designing the combined recogniser. The conceptually simplest is to merge all the automata corresponding to each token class into one. This is the approach we take here. The combined automaton for the token classes is as shown in the following figure:

The Combined Automaton

Recognising the Next Token

The central function in lexical analysis is the stateful procedure that begins consuming character upon character until it can consume no other. At that point it has to make a decision as to whether it has been able to recognise a valid token. If yes, that token is returned; otherwise, an error is announced. So, at the high level, the algorithm goes like this:

Pseudocode for the procedure that gets the next token

Architecture and Implementation

Now, let’s take a look at the implementation that we have done. The system has been designed within a Scanner class, which encapsulates an instance of DFA class.

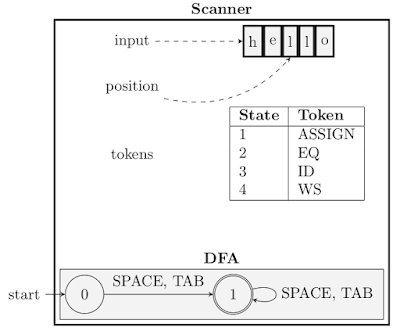Architecture of the Lexical Analyser

Class DFA

DFA class provides the basic API for creating a deterministic finite state automaton. An instance is created by specifying the list of state IDs (which are integers), the initial state ID, and the list of final states ID. The transitions are later added to the DFA using the add transition method in a very user-friendly manner. Internally, the DFA has been designed like a directed graph using adjacency list style connections.

Class Scanner

The Scanner class implements the functionalities of the lexical analyser. It keeps account of the input string, and the progress of the lexical analysis through this string. It actuates the DFA by feeding it one character at a time, and makes the decision regarding acceptance or rejection of the input string at appropriate
times. the next token method returns the next token beginning at the current position on the input string. scan method returns all the tokens contained in the input string, by making repeated calls to next token.

Code

The code for the lexical analyser can be found in this link. In fact, as of the current date, the code contains a slight enhancement to the lexical analyser described here, in that it is also able to distinguish between identifiers and keywords. The scanner is implemented in KWScanner class which simply extends the Scanner class with the required capability.

This code is likely to keep evolving beyond what is described here. The latest version of the code can be found in this link. 

User Instructions

The executable la is created by running make. la can be run simply without provided any command line arguments.

Navigating the Code

The main function is in the file la.cpp. The above example is implemented in the test case function t3. In t3, we create an object dfa of type DFA. We construct it to resemble the DFA shown in figure above.